时间过得真快，转眼已到九月中旬。九月是收获的季节，也是播种希望、孕育新生的季节。

在这个缤纷多彩的季节里，小月童仲思宇、胡心钰带着同一道好题——程问题之二次相遇问题，共同走进“月童说题”，让我们赶紧打开视频，去聆听他们的不一样的精彩讲解吧！

01经典好题

甲、乙两车同时从A、B两地出发相向而行，两车在离B地64千米处第一次相遇。相遇后两车仍以原速继续行驶，并且在到达对方出发点后，立即沿原路返回，途中两车在距A地48千米处第二次相遇，问两次相遇点相距多少千米？

第一步：根据题意，画出线段图。线段图是解决行程问题的好帮手，不仅可以将题意形象地表示出来，还能直观、清楚地反映出数量之间的关系，容易找到解题方法。我们先根据题意画出线段图：

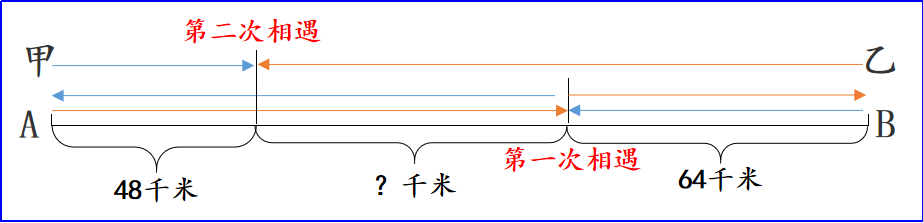
为了让大家更清楚地看出题目中的数量关系，我们还可以把上面的线段图调整一下：

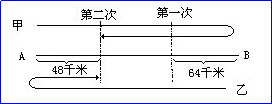
第二步：利用线段图，分析数量关系。

从图中可以清楚地看出：第一次相遇时，甲、乙两车正好走了一个AB全程，此时，乙车走了64千米；第二次相遇时，甲、乙两车共走了3个AB全程，因此，我们可以理解为乙车共走了3个64千米。由上图可知：乙车行驶的总路减去一个48千米后，正好等于一个AB全程。

02视频讲解

①求AB两地间的距离。

64×3-48

=192-48

=144（千米）.

②求两次相遇点的距离。

144-48-64＝32（千米）

答：两次相遇点的距离为32千米。

同学们，我们的讲解你们听明白了吗？

你们能用学到的本领尝试完成下面的挑战题吗？

03挑战自我

1.甲、乙二人以均匀的速度分别从A、B两地同时出发，相向而行，他们第一次相遇地点离A地4千米，相遇后二人继续前进，走到对方出发点后立即返回，在距B地3千米处第二次相遇，求两次相遇地点之间的距离。

2.甲、乙两车同时从A、B两地相向而行，在距B地54千米处相遇，它们各自到达对方车站后立即返回，在距A地42千米处相遇。两次相遇地点相距多少千米？

3.在一个圆形跑道上，甲从A点、乙从B点同时出发，反向而行，8分钟后两人相遇，再过6分钟甲到B点，又过10分钟，两人再次相遇，则甲环行一周需要多少时间？

04上期答案  

1.一列快车和一列慢车相向而行，快车的车长是280米，慢车的车长为385米，坐在快车上的人看见慢车驶过的时间是11秒，那么坐在慢车上的人看见快车驶过的时间是多少？

2.快、慢两列车的长分别是150米和200米，相向行驶在两条平行轨道上。若坐在慢车上的人见快车驶过窗口的时间是6秒，那么坐在快车上的人见慢车驶过窗口所用的时间是多少？

3.A、B两点相距30厘米，甲、乙两根细绳在玩具车的牵引下从A、B两点同时出发相向而行。甲绳长151厘米，前进速度每秒2厘米；乙绳长187厘米，前进速度每秒3厘米。如果出发前两绳尾端同时被点燃，甲绳燃烧速度为每秒1厘米，乙绳燃烧速度为每秒2厘米。两绳从相遇到完全错开共需要多少时间？

T1：

280÷（385÷11）＝8（秒）

答：坐在慢车上的人看见快车驶过的时间是8秒。

提示：在这个过程中，对方的车长＝两列车的速度和×驶过的时间，而速度和不变。

T2：

两车的相对速度为：

150÷6=25（米/秒）

快车上人人看慢车用的时间为：

200÷25=8（秒）

答：坐在快车上的人见慢车驶过窗口所用的时间是8秒。

T3：

30÷（2+3）=6（秒）

（151+187）÷（1+2）×6=320（厘米）

320÷（2+3+1+2）=40（秒）

答：两绳从相遇到完全错开共需要40秒。

提示：这道题需要把它们的行程过程分为两个阶段，相遇前和相遇后。相遇前的速度和是每秒2+3=5厘米，相遇后的速度和是每秒2+3+1+2=8厘米。